Explaining Behavior 5: Handling Anomalies

On puzzle solving and ad-hoc adjustments

Feb 11, 2023

If you’re reading this, I appreciate your interest!

Part 5 in a Series. Previous entries: 1. What is Theory? 2. Styles of Explanation. 3. The Deductive Model. 4. Testability. 4.5. (Paid Only) Teaching Testability

In the last installment we covered the importance of testability: To learn whether an explanation is correct, it must be an idea that it could, in principle, contradict the facts. If some conceivable observation could disprove it, the theory is testable by way of being falsifiable.

Karl Popper emphasized falsifiability because theories can’t be verified by the facts they explain. Even with perfectly accurate evidence, proving theories is impossible. The problem is logical. There’s an asymmetry in how truth goes through deductive systems: The truth of the conclusion doesn’t prove the truth of the premises, but the falsity of the conclusion does show us the falsity of the premises.

Well, of at least one of the premises. And here’s where a complication comes in.

Testing a System

When we deduce a conclusion and that conclusion is wrong, we have to decide which premise is the culprit. It could be they’re all wrong, or it could be just one of them is.

Consider an example. Durkheim’s theory of egoistic suicide tells us that suicide decreases with social integration. We consider marriage something that provides social integration. Therefore, we expect married people to have lower rates of suicide.

We apply this reasoning to a study of young women in rural Taiwan in 1960. These young married Hokkien women are more integrated, these young single Hokkien women are less integrated. Therefore there will be more suicide among the young single women.

But it turns out that’s not the case. A young Hokkien woman’s risk of suicide rises greatly when she is married, and young married women have the highest suicide rate of any demographic category.

Let’s assume we’re confident in the evidence. Do we then conclude that our theory was wrong, and that social integration has no effect on suicide? Or is the problem instead our idea that the married women had greater integration? In considering which to jettison, we ought to turn to additional evidence.

Let’s say we have a lot of studies confirming predictions of Durkheim’s theory using various measures of social integration (I believe we actually do). In this case, declaring the theory false because of one missed prediction is a bit hasty. I don’t know if this exactly what the rationalists mean by having “strong priors,” but generally when you have a ton of evidence for P you don’t immediately throw it out at the first report of Not-P.

So let’s turn out attention to the other assumption: That married people are more integrated. Maybe this needs some revision or qualification. Sure, by definition marriage creates a social tie and an institutional involvement. But could it somehow cut off other ties and involvements?

Let’s turn to the facts on the ground in rural Tawain. How exactly does marriage work in this setting? Well, the ethnographers say it involves a women ritually cutting all relations with her birth family and moving in with to her husband’s household, often at great distance from her home, kin, and friends. The marriage was arranged, and so she’s a virtual stranger even to her husband as well as an outsider to the surrounding community. She’s basically a new domestic servant with no close ties.

I think under these conditions it might be safe to say marriage, at least initially, is a net decrease in social integration.

Thus we don’t take the suicide data as evidence that the general proposition was wrong, but as evidence we were wrong about the conditions we were applying it to. Maybe we qualify the idea that marriage provides integration, but we don’t need to revise the theory that lower integration increases suicide.

This is always an option when we face disconfirming evidence. And it’s actually something science does quite a lot.

Explaining Away Contradictions

In The Structure of Scientific Revolutions, historian of science Thomas Kuhn distinguished between revolutionary science, when drastically new theories and approaches overturned the old ones, and normal science, the piecemeal, incremental accumulation of knowledge.

Normal science is, naturally, the more common of the two. It is the usual activity of people working in scientific fields. Kuhn notes that much of this activity has a puzzle-solving character. The established theories in a field solve enough problems to inspire some faith that they’re correct, but they don’t solve every problem. They leave mysteries and exceptions. This includes facts that don’t seem to match the theories predictions.

In real life, when scientists have a theory that has successfully predicted A through D, they don’t throw it out as soon as it incorrectly predicts E. Instead, they seek additional information to figure out how to make these anomalous facts consistent with their theory.

Here’s a historical example: Newton’s theories of gravity and motion did a good job explaining the orbits of the planets. You could use them to calculate where in the sky a planet should be visible at a given time. But when astronomer Alexis Bouvard used these principles to predict the orbit of the planet Uranus, there were some major errors – it showed up in times and places that did not match the predictions of the theory. In a naïve application of Popper’s doctrine, the theory had been falsified. Time to give up on Newton and go back to the drawing board.

But this isn’t what happened. Bouvard instead wondered what other premises he had to add to his deductive system in order to make it yield the right prediction. He assumed Newton’s theories were correct and instead changed his ideas about the initial conditions. One condition that he could add to this model was the existence of another planet out there beyond the orbit of Uranus, whose gravity was exerting enough pull on Uranus to account for the deviations. Thus he hypothesized the existence of a new planet.

Astronomer John Couch Adams then used Newton’s laws, along with the observational data about Uranus’s actual orbit, to calculate the location of this previously unobserved planet. And this is how Neptune was discovered: Scientists facing an incorrect prediction assumed the theory must be right and sought out the facts necessary to keep it right.

We see in this example the usefulness of not throwing out a theory at the first sign of trouble. Virtually no theory makes 100% correct predictions, and a lot of scientific progress comes exactly from explaining away the apparent exceptions.

This doesn’t undermine the importance of having a testable theory – if the theory wasn’t clearly falsifiable, how would we ever recognize these exceptions and realize that they’re problems in need of solving? Clear and unambiguous predictions are valuable exactly because they allow such friction with observation, and the friction is productive.

Ad-Hoc Adjustments

This insight shows a way in which even a clear and unambiguous proposition has wiggle room to avoid falsification. Philosopher Imre Lakatos suggested we view every theory as a network of ideas with a core and periphery. At the core are the really crucial assumptions, the basic laws of nature or basic assumptions of the field. In physics this would be things like the conservation laws. At the periphery are ideas he called auxiliary hypotheses that are less fundamental and more easily sacrificed. When faced with contradictions, people try to preserve the core by making adjustments to the periphery.

Philosophers Duhem and Quine went so far as to say we can always preserve any idea in the face of any evidence, provided we’re willing to make the necessary adjustments elsewhere in our system of beliefs.

This brings us back to the problem we noted in the last installment: That a theory can be made untestable by the behavior of true believers, who with enough determination can stretch it to fit any conceivable evidence. Only now we see that this ridiculous unscientific behavior sits on a continuum with a valuable scientific activity. Life is complicated like that.

Recall that Popper recognized this problem, and that his solution was methodological: Don’t evade falsification. But of course he recognized the need to defend and revise theory. So he gave the more detailed answer that adjustments are fine, as long as they themselves add testable content. The Neptune hypothesis is good because it was itself testable, and added a precise and novel prediction to the theoretical system. As adjustments go, it was a good one. A bad revision would be an ad-hoc adjustment – a “just this case” exception. “Here’s a black swan.” “All swans are white – but that one.” You’ve saved your white swan theory, but you’ve added nothing to our knowledge.

On Simplicity

Avoiding excessive and ad-hoc adjustments might be an under-appreciated function of the value scientists place on simplicity (or parsimony or elegance). This preference is sometimes summarized in a precept known as Occam ’s razor – all else equal, the simplest explanation is the most likely. One reason that Occam’s razor works as a heuristic is that attempts to evade falsification by piling on ad-hoc adjustments tend to complicate things.

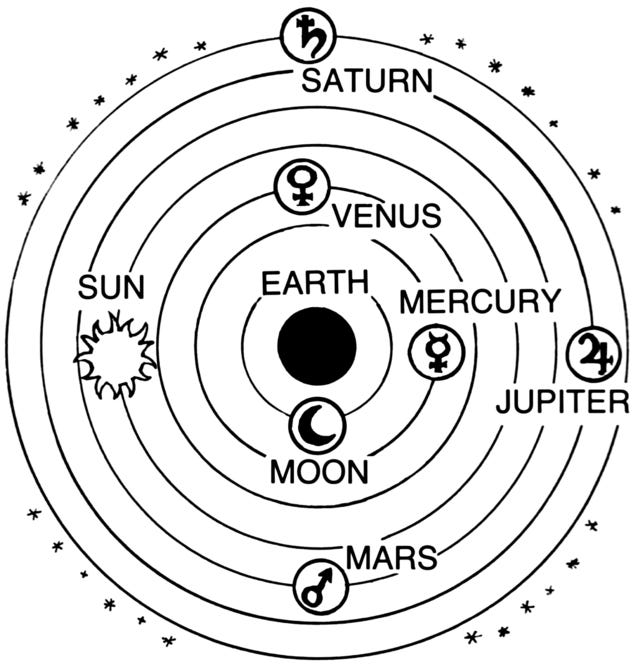
The classic example here is the Ptolemaic model of the solar system. The work of ancient astronomer Claudius Ptolemy, it tried to make sense of the observations of the night sky by positing a system where the sun and planets all revolved around the earth in circular paths.

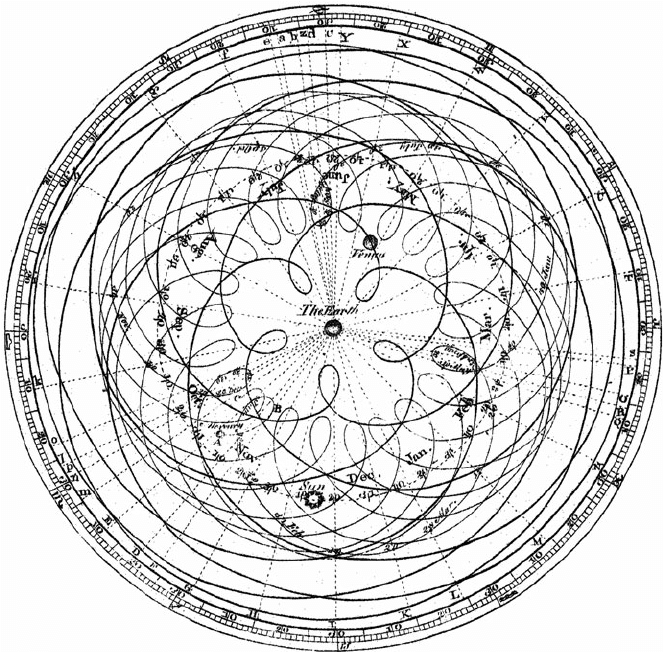
It actually did make sense of astronomical observations. But there were exceptions, anomalies. This isn’t such a big deal, as we have seen – it’s common for scientific theories to have anomalies, and for a lot of scientific work to go into explaining them away. But the problem was that these contrary observations kept piling up, and the way of dealing with them was to make ad-hoc adjustments to the model in the form of adding epicycles – little orbits within the orbits, loop-di-loops the planets and sun made on their journeys.

New observations say the planet was not in the predicted place? Time for a new epicycle. Mo’ cycles, mo’ cycles, mo’ cycles. By the time it finally fell to its competitor, the Copernican sun-centered model, it had grown into a bit of a monster.

Indeed, when Copernicus first advanced his alternative theory he couldn’t claim his matched the facts better, he could only claim it did so more simply. But time would show his model was more correct as well.

One can perceive a similar multiplying of assumptions in less scientific ideas than Ptolemaic astronomy. Consider contemporary theories that the earth is flat or the moon landing was a hoax. I’m sure there are Youtubers who can walk you through long strings of implausible ideas, each created to defend against criticisms of some previous implausible idea.

Next installment: Part 6: Paradigms. We switch from philosophy of science to covering actual theories in Part 7: Phenomenology. Followed by Part 8: Motivational Theory, Part 9: Opportunity Theory.

For paid subscribers, I have installments with teaching materials. See Part 4.5: Teaching Testability, Part 6.5: Exercises on types of theory, propositions, and deducing predictions, and Part 8.5: Exercises on applying and evaluating phenomenological and motivational theories.

Bullfish Hole

Discussion about this post