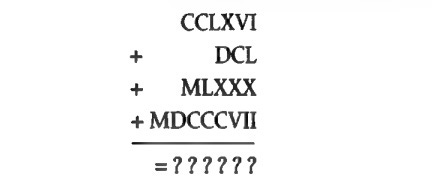Books: The Universal History of Numbers

From Prehistory to the Invention of the Computer

If you’d like to support Bullfish Hole, you can leave a tip at this Stripe link. Or become a subscriber with the button below.

Sometime in the 1970s, French math teacher Georges Ifrah was thrown off by his students asking questions about the origin of numbers.

“Sir,” said one of them, “where do numbers come from? Who invented zero?” Another followed up with “Sir! Can you tell us how the Romans did their sums? I’ve been trying to do multiplication with Roman numerals for days, and I’m getting nowhere at it!”

Ifrah then made the quite natural decision to quit teaching and dedicate years of his life to compiling a global history of numbers.

The result is The Universal History of Numbers, a 600-page tome that goes from the Stone Age up to the book’s 1981 publication date. It’s dense, detailed, and sometimes a bit disorganized, bouncing as it does between civilizations or between particular problems to do with numbers — including chapters on how money evolved and mystical numerology. There’s even an entire chapter devoted to being a dictionary of Sanskrit number terms.

But the whole thing drives home one central point: Our modern system of numbers and counting is a miracle of cultural evolution. While we usually think of technology as something that happens when we apply math, we’re only able to do math because of an amazing cultural toolkit for quantifying the world.

Numbers as we know them are a technology that evolved late in the history of humanity and that didn’t spread around the globe until recently. As a result, our young children routinely do what some fairly well-educated men in the Europe of 1500 could not:

“I was borne and brought up in the Countrie, and amidst husbandry: I have since my predecessours quit me the place and possession of the goods I enjoy, both businesse and husbandry in hand. I cannot yet cast account either with penne or Counters.”

These words were written by one of the most learned men of his day: Michel de Montaigne, born 1533, was educated by famous teachers at the College de Guyenne, in Bourdeaux, travelled widely thereafter, and came to own a sumptuous library. He was a member of the parlement of Bordeaux and then mayor of that city, as well as a friend of the French kings Francois II and Charles IX. And he admits without the slightest embarrassment, that he cannot “cast account” — or, in modern language, do arithmetic!

And Montaigne lived in a time where modern numbers had been introduced and widely adopted. As we go back deeper into the history of humanity, we find a world where numbers as we know them did not exist at all.

A World Without Number

The first anatomically modern humans surely had the ability to perceive quantity, since other animals do as well:

Domesticated animals (for instance, dogs, cats, monkeys, elephants) notice straight away if one item is missing from a set of familiar objects. In some species, mothers show by their behavior that they know if they are missing one or more of their litter. A sense of number is marginally present in such reactions.

At its simplest, there’s not a lot of daylight between quantitative and qualitative discrimination: Noticing the pile got smaller is just a special case of noticing it looks different. But some animals, including some species of birds such as goldfinches and crows, can reliably discriminate between specific quantities. The hitch is that the quantities have to be small and the differences between them relatively big:

It only works in goldfinches when the “moreness” and “lessness” is quite large; the bird will almost always confuse five and four, seven and five, eight and six, ten and six. In other words, goldfinches can recognize differences of intensity if they are large enough, but not otherwise.

It seems like humans who haven’t been trained in counting can’t do much better. Hence small children who haven’t yet learned numbers can distinguish one, two, and more-than-two at a glance, but have trouble distinguishing four from five. Even you, who have the cultural tools for distinguishing higher numbers, have trouble doing it without consciously counting. Quick test: Glance at the images below and say, without counting, how many objects are in each group:

Most can easily pick out singles, pairs, triplets, and many spot sets of four. But people have trouble telling at a quick glance whether there’s five or six, six or seven, seven or eight. Unless the objects are arranged in a familiar pattern like the dots on a die, your eye’s ability to perceive specific numbers tops out at around four.

That’s about the limit of our natural ability to numerate. Beyond four, quantities are vague, and our eyes alone cannot tell us how many things there are. Are there fifteen or twenty plates in that pile? Thirteen or fourteen cars parked along the street?

This limit of four looks like the hard-wired base-level of human numeracy, and many human cultures haven’t gone much beyond it. Several tribal societies don’t have names for specific quantities over two:

The Botocudos had only two real terms for numbers: one for “one,” and the other for “a pair.” With these lexical items they could manage to express three and four by saying something like “one and two” and “two and two.” But these people had as much difficulty conceptualizing a number above four as it is for us to imagine quantities of a trillion billions. For larger numbers, some of the Botocudos just pointed to their hair, as if to say, “there are as many as there are hairs on my head.”

The Aranda are similar: They have terms for “one” and “two,” and can combine them to express “three” and “four,” but for anything larger they use terms like “a lot” and “many.”

The same goes for the Murray Islanders, the Torre Strait Islanders, and others. “One, two, many” counting systems aren’t unusual, and likely there was a time when no human group had any numbers above four.

Counting Before Numbers

But that didn’t mean people couldn’t count past four. It turns out that people were counting and measuring large quantities long before they had numbers for them. It wasn’t numbers that gave us counting, but counting that gave us numbers.

The trick for counting without number is mapping one object onto another.

Suppose a shepherd wants to make sure that he hasn’t lost any sheep during the day. So, as he lets them out of their pen in the morning, he puts a pebble in a sack for each one that walks past him. Then when he brings them back in the evening, he takes a pebble out of the sack for each one that goes back in the pen. If there’s any pebbles left in the sack, he’s missing sheep.

Thus our shepherd can tell the difference between having 51 sheep or only 50, despite not having any concept of either number.

People all around the world quantified things this way for a very long time, keeping track of the number of this or that by using pebbles, sticks, tally marks, or body parts.

Body Counting

The most obvious and convenient thing to count on is our own bodies.

Most cultures use the fingers; some add the toes. Some use each finger joint, allowing them to count to thirty with just two hands. Some add the elbows, shoulders, ears, eyes, nose, mouth, knees, or ankles.

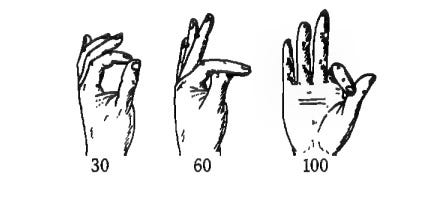
Ifrah has a whole chapter just on different systems of finger counting, drawing on everything from contemporary ethnographies of tribal people to how counting is depicted in ancient Egyptian hieroglyphics. In a few cases, finger counting evolved into something closer to sign language, with distinct handshapes for numbers like sixty, one hundred, or one thousand. Such was the case in ancient Rome, in Europe during the Middle Ages, and in the Islamic world:

A qasida of the Persian poet Anwari (died 1189 or 1191) praises the Grand Vizir Nizam al Mulk for his precocity in arithmetic: “At the age when most children suck their thumbs, you were bending the little finger of your left hand” (implying that the Vizir could already count to a thousand).

In Europe, people developed sophisticated techniques for doing math on the fingers:

Barely four hundred years ago, a textbook of arithmetic was not considered complete without detailed explanations of this system. Only when written arithmetic became widespread, with the adoption of the use of Arabic numerals, did the practice of arithmetic on hands and fingers finally declined.

Tally Marks

Tally marks are also a near-universal, and we have archaeological evidence that people have been using them for at least 40,000 years. For instance, one Cro-Magnon site revealed a notched wolf bone, with the notches arranged in evenly spaced groups of five. The artifact wasn’t so different from one Ifrah saw used in a country bakery in Dijon in the 1970s:

This is how it is done: Two small planks of wood, called tailles, are both marked with a notch each time the customer takes a loaf. One plank stays with the baker, the other is taken to the customer. The number of loaves is toted up and payment is made on a fixed date. . . . No dispute over the amount owed is possible: Both planks have the same number of notches, in the same places.

Some peoples preferred knots in string over grooves in wood. The Inca of Peru famously developed this into a fairly sophisticated device called the quipu, a cord hung with colored strings that was essential in government bookkeeping:

Quipus are so simple and so valuable that they continued to be used for many centuries in Peru, Bolivia, and Ecuador. In the mid-nineteenth century, for example, herdsmen, particularly the Peruvian Altiplano, used quipus to keep tallies of their flocks. They used bunches of white strings to record the numbers of their sheep and goats, usually putting sheep on the first pendant string, lambs on the second, goats on the third . . . .

Pebbles and Tokens

The other big counting technology of the ancient world were objects like pebbles and counting tokens made from clay.

Pebbles and tokens were important enough in the classical world that our English word calculate comes from the Latin word calculus, meaning pebble:

Because the Greeks and Romans taught their children to count and to perform arithmetical operations with the help of pebbles, balls, token, and counters made out of stone . . . . their word for “doing pebbles” (calculation) has come to refer to any of the elementary arithmetical operations.

When Pythagoras was investigating squares (like two times two), he was literally making square formations of counting stones.

Calculating Without Numbers

As primitive as they are, one can keep track of surprisingly large quantities with these kinds of mapping systems. One can even approximate operations like addition and multiplication.

I’ll give a simplified version of Ifrah’s hypothetical example.

Suppose a chief has recently won a battle against a rival, and as part of the peace settlement demands a certain amount of compensation for each soldier that he lost. But how many soldiers did he lose? Our chief used the technique (that at least one culture really did use) of having each warrior deposit a pebble in a container on his way out of the village and reclaim the pebble when he returned.

We’d say he has sixteen pebbles, and he lost sixteen men. But the chief knows of no number bigger than “a pair and a pair.” He only knows he’s got a pile of many unclaimed pebbles, and wants compensation for each one.

So the chief tells his envoys that for each unclaimed pebble, he wants [goes through a finger-counting sequence on one hand] this many pearl necklaces, and [goes through a finger counting sequence on both hands] this many fox pelts. We’d say he asked for five necklaces and ten pelts for each man, but the chief doesn’t know those numbers, either.

Then he dispatches three envoys — one in charge of counting pebbles, one in charge of counting necklaces, and one in charge of counting pelts. When they arrive, they stand before the rival chief’s court. First, Necklace Guy stands up and says, “give me one necklace for each finger I point to,” and keeps pointing to fingers until he’s got as many necklaces as fingers on one hand. Then Pelt Guy steps up and does the same thing, getting as many pelts as fingers on both hands. When they’re both finished, Pebble Guy takes one pebble from the bag and tells them to repeat the operation. They keep going until there’s no pebbles left in Pebble Guy’s bag.

The result is they get five necklaces and ten pelts for each of the sixteen men. It’s effectively the same as if they’d multiplied sixteen by five to determine they need eighty necklaces and sixteen by ten to arrive at one hundred and sixty pelts. But no one involved knows any of these numbers or what multiplication means.

From Counting to Numbers

It’s hard for us numerate people to truly wrap our head around counting without numbers.

Sure, we still count on our fingers nowadays, but the fingers are just placeholders for number concepts. For instance, when my wife and I are trying to figure out how many people are coming to the party, we start naming guests while holding up a finger for each one, so that we don’t lose track while thinking of the next name. But once we’re done, we have a concrete number — say, seventeen — and don’t need to resort to our fingers again. It’s seventeen people; we’ll need seventeen chairs and seventeen cheeseburgers. If one person cancels, we just need sixteen of each.

When we do this, we’re operating at a level of abstraction people without numbers just don’t share.

In the body counting system of pre-numerate people, there’s a standardized progression for counting — such as always starting with the right thumb and moving to the right pinky — and there’s some standardized counting gestures. The body parts don’t indicate numbers outside of this sequence with gestures. You can’t just say “right pinky” and have people treat it like we would treat the number “five.” They’d just ask, “what about your right pinky?”

The number doesn’t yet exist independently of the counting. For these people, the only way to verify whether they’ve got the same number of chairs or burgers as guests is to go through the counting sequence for each and verify that they end on the same body part.

But counting does, at least in some societies, lead to the evolution of abstract numbers. Ifrah describes the evolution in three stages.

Stage 1 we’ve just explored: People have no number words higher than three or four, and counting larger quantities requires mapping onto concrete models like fingers or stones or tally marks.

Stage 2 arises when the counting words come lose their concrete connotations. There’s linguistic divergence between the term we use to refer to the body part during the counting sequence versus when referring to it otherwise.

Ifrah doesn’t get into it, but I imagine it starts with people counting in a particular tone or rhythm or inflection to make it clear they’re counting, and the pronunciation during counting gradually gets distinct enough that one day someone in a hurry, instead of going through the whole sequence, pronounces “pinky finger” in the counting way and everyone gets he means “counting pinky,” not “regular pinky.”

Whatever the details, the term for some body part does eventually comes to mean a definite quantity rather than the part itself. Ifrah goes over linguistic evidence that basic number names do often have their origin in names for body parts.

At the end of Stage 2, the culture has number terms above three or four, and an abstract conception of a number as something applicable to various objects: People can say that five people need five plates and five chairs.

Stage 3 proceeds with developing a proper system of nomenclature for numbers. The first few basic numbers in the sequence might betray their ancestral roots as terms of fingers or whatnot, but people run out of those pretty quick as they work their way up to higher values. And imagine if we had to keep inventing new idiosyncratic names for each number we encountered on the way to infinity — our whole vocabulary would be nothing but number terms!

“The solution,” Ifrah writes, “is found is a remarkable example of human ingenuity.”

Base Numbers

That solution is to create a hierarchical relationship between sets of numbers. Some are base numbers, that act like the floors of the building, while the other numbers are the steps up the stairs.

Our own default number system has a base of ten. Once you reach ten, you start repeating one through nine, only with a ten stuck in front to let you know that the number is ten-and-one (eleven), ten-and-two (twelve), and so on. Once you pass nineteen, your base goes up to twenty (two tens) and you start counting from one again: Twenty-one, twenty-two, and so on.

In English, the names of the teens don’t fit the pattern, but otherwise the repetition is obvious: After twenty comes twenty-one, after thirty comes thirty-one, and so on up the orders. I taught my own two young children to count, and once they got the teens straight, it was pretty quick to get them to one hundred. The only new number words they had to learn were for the bases (twenty, thirty, etc.) and then apply the one-through-nine counting they’d already learned before.

Base numbers also evolved out of the older systems of counting with fingers and pebbles and knots. For instance, maybe every time I count to five on my left hand, I raise a finger on my right hand to indicate I’ve got one group of five, then start over counting on my left hand until I get another group of five. This is at least an implicit use of a base of five, and in spoken language it might sound like “It comes out to two fives and three!”

Bases vary across cultures. Some, like the Carib or Guarani or Fulah, do indeed have base five, almost certainly the result of people counting on one hand in the way I just described. The most common base is ten, found everywhere from China to India to the Incans, and it surely has its origins in people having ten fingers and tending to count on both hands. But people in some cultures must have counted on their toes as well — peoples such as the Ainu and Zapotec have a base of twenty.

There are still vestiges of other bases in our modern system, too. Traders long found it useful to work in a base of twelve, which makes it easier to calculate quarters and thirds as well as halves. And to this day we still buy donuts and eggs by the dozen or gross. And the bizarre Sumerian base of sixty still lives on in how we measure time (sixty seconds to the minute, sixty minutes to the hour) and angles.

There are trade-offs involved in whatever base a society uses. A low base makes for fewer number terms but requires longer combinations of them to express big numbers. A high base has the opposite problem. And different bases have different mathematical properties. For instance, if we used a prime number like 11 as base, most fractions would be irreducible.

Base ten isn’t perfect and isn’t necessarily what a math nerd would have designed from the ground up, but it works well enough and avoids problems of much bigger or much smaller bases.

The base of sixty used by the Sumerians is so weirdly and uniquely big, and so unconnected to easily counted body parts, that its origin is a historical mystery. Ifrah’s theory is that it was a way of reconciling two cultures. Ifrah supposes that the Sumerians migrated into a region where there was already an indigenous population whose counting system used a different base. One culture, it doesn’t matter which, had base five system, the other a base twelve system. The best middle ground for people brought up in either system was base sixty, of which five and twelve are factors.

Originally a kludge meant to reconcile people trained in different finger-counting techniques, the learned men of Sumer soon discovered the system was useful for astronomy and geometry and came to view the number sixty as something special enough to be named after one of their gods.

Writing Numbers

So far, I’ve been going out of my way to write numbers with words instead of using numerals, because having a word for numbers and having distinct symbols for them are two different things.

Written number symbols, where they’ve evolved, sometimes come from the physical technologies of counting. It’s easy enough to see how tally marks can evolve into numerals. Consider the Roman system: One = I, Two = II, Three = III. These numerals match the notches carved on prehistoric artifacts, and even in the heyday of the Roman Republic its numerals were already a living fossil, a relic of the Stone Age.

In other cases, the symbols started with counting tokens. In ancient Mesopotamia — where they did everything with clay — one kept count with clay tokens of various sizes and shapes to indicate different amounts. This developed into a record-keeping system. If you wanted an official record of the sale of forty-eight animals, you went to a scribe who counted the appropriate tokens to represent that amount and then sealed them in a hollow clay ball. Then he’d put some makings on the outside of the ball to indicate which sale record the ball contained, and if you ever had a dispute about payment or ownership you could call him into court to break the ball and recount the tokens.

Sooner or later, accountants began putting marks on the outside of the ball that indicated how many and what kind of counting tokens were inside, so they could consult their record without breaking the ball. From there it was a quick jump to abandoning the ball altogether and just keeping the record on clay tablets, with the images of the tokens evolving into numerals.

Still others, like the Attic Greeks, started with written words for the numbers and got their numerals by abbreviating the words.

Either way, systems for writing numbers ran up against the problem of how to express very large ones.

One solution is the additive principle, where you write big numbers as the combination of smaller ones. The Roman system works in part by the additive principle: V is five, and I is one, so VI (five and one) is six, VII (five and one and one) is seven, and VIII (five and one and one and one) is eight. But they also complicated things by introducing a subtractive principle, where IV (five minus one) is four and IX (ten minus one) is nine.

You might see how this becomes cumbersome if you want to write really big numbers. Suppose that your language doesn’t have words for big units like thousand, so you verbally express the idea of a thousand by saying “a group of ten hundreds” and express it in numerals by writing the symbol for hundred ten times in a row. For five thousand, you’d need to write the hundred symbol fifty times in a row.

Even if your culture did have a word for thousand or ten thousand, writing 15,567,234 might take you half a sheet of parchment and would be difficult as heck for your audience to read, given that — as we’ve established — people can’t tell from a glance whether there’s eight or nine or ten of that symbol in a row.

Most ancient cultures, Irah says, used some version of the additive principle. But he sees the principle itself as an evolutionary dead end — if you stick to it, you’ll never get a number system really useful for doing calculations. For in addition to making your number expressions huge and clunky, it makes it nearly impossible to do the kind of written calculation that we now take for granted.

It never occurred to me before, but this is another way in which modern numbers are an amazing technology. I can sit down with a piece of paper and follow the rules I was taught in school to add or multiply two large numbers — numbers I could never work with in my head, but know how to work with on paper.

Now try doing this with Roman numerals and see how far you get.

In earlier periods, mathematicians working at levels of abstraction and complexity that I can’t comprehend still weren’t able to do basic sums on paper (or parchment or clay or whatever they had). Without the technology of our modern system for writing numbers, they had to use physical technologies to plug the gap.

Math Hardware

For a lot of history, written numbers were pretty useless for calculation, and scholars had to keep relying on techniques descended from the old counting stones.

This is why the Greeks and Romans still used calculi and called mathematics calculation long after they had numerals. As mathematics advanced, the use of counters and tokens only got more complex. The result was the height of premodern calculating technology: The abacus.

The abacus was found from Rome to Babylon to China. Their exact nature and construction varied, but all consisted of some sort of counting tokens, organized in groups (to represent units like ones, tens, and hundreds), and mounted on a structure that allows one to move them around. For whatever math operation one needs to perform, one follows a certain procedure on the abacus, moving the counters of different units wherever they need to go.

You can find Youtube videos demonstrating their operation.

Though Roman numerals might be the least practical system of any ancient civilization, the Romans did a lot of calculation. They did so much that they invented a little portable pocket abacus: “a small metal plate, with a certain number of parallel slots (usually nine). Each slot was associated with an order of magnitude, and mobile beads could slide along them.”

The ancient Chinese developed a much more sophisticated number system, with a base of ten and thirteen basic signs. They could write big numbers fairly efficiently and developed advanced mathematics, but they still couldn’t do written math. They too relied on an abacus, and skill with one was an important quality in officialdom. Their civilization produced a few different versions of the abacus, the last of which remained an important piece of technology well into the 20^th century. At the time Ifrah was writing in the late 1970s, it was still to be found sitting next to the cash register in Chinese shops and hotels.

Abacus skill also remained important in twentieth century Japan:

“Westerners are invariably astonished at the speed and dexterity with which the most complicated calculations can be done on an abacus,” including a case in 1945 in which a Japanese abacus champion beat a US serviceman operating an electric calculator in a math competition.

Which reminds me that American physicist Ricard Feynman had an amusing story about how he defeated a Japanese abacus expert using his extensive familiarity with numbers.

It took electronic calculators to finally kill off the abacus in most parts of the world. But by then the use of the abacus for basic arithmetic was already on the wane, replaced by written math. New software had made the old hardware obsolete for many uses. The new software was the modern system of numbers.

Modern Numbers

In the West, we call the numerals we use — 1,2,3, etc. — Arabic, because they diffused into Europe via Dar al Islam. But though the Arabs modified and passed them on, the numbers originated in ancient India, along with the number system that beat out the competition.

Ifrah views the modern system as a damn-near perfect technology. Sure, we could play around with other bases, or maybe tinker with the graphical form of the symbols. But he can’t imagine changing the basic structure of the thing: It is “mathematical perfection.”

So what’s so special about the modern number system?

One crucial feature is that it abandons the additive principle. Instead, it is a multiplicative system: Rather than expressing thousand by writing “hundred” ten times, one writes “ten times a hundred.”

The multiplicative principle itself improves efficiency. More importantly, though, it opens the door for another innovation: The positional system.

In a positional system, what quantity a numeral refers to depends on its position in the string of numerals. The “4” in “451” means “four hundreds,” but in 541 it means “four tens” and in 154 it means just “4.”

The positional system produces a great gain in economy of expression: You only need to learn a small number of basic number symbols (1-9) and then you can write down every possible number from here to infinity. And you can do it without all the repetition of symbols necessary in an additive system, or even without bothering to write out the multiplication implicit in the system.

As Ifrah puts it:

Nowadays, this principle seems to us to have such an obvious simplicity that we forget how the human race has stammered, hesitated and groped through thousands of years before discovering it, and that civilizations as advanced as the Greeks and the Egyptian completely failed to notice it.

The positional principle cropped up independently in multiple civilizations — in Babylonia about 4,000 years ago, in China about 2,000 years ago, and among the Mayans about 1,000 years ago. But these systems had other limitations in their way of writing numbers (like writing three as “1,1,1”) that kept them from making good use of it.

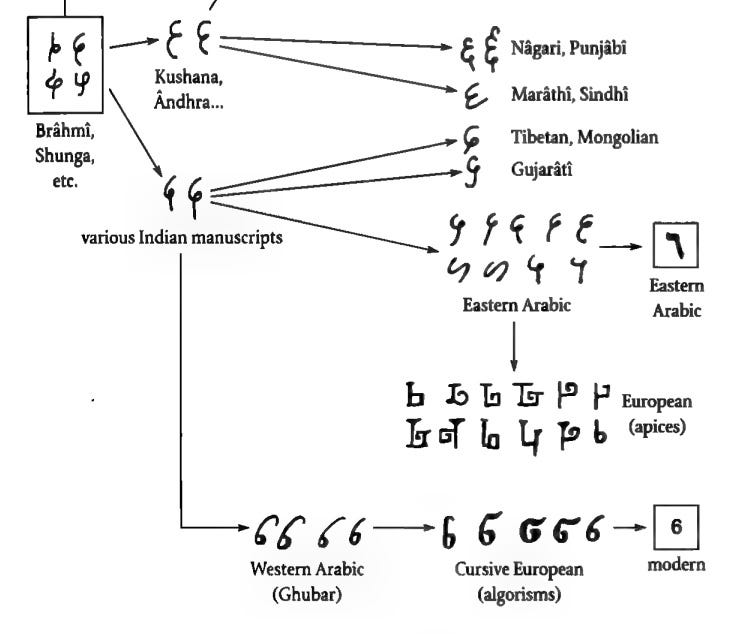
The positional system needed to be wedded to a good system of numerals: A small number of basic symbols, each such an abstraction that people treated them as pure numbers and not tally marks. Our symbols themselves come from Brahmi writing system of ancient India.

You can see recognizable ancestors of our numerals on stone proclamations from the reign of the philosopher king Ashoka around 235 B.C. They were probably old even then, and while they likely have their own origin in tally marks, by this time they’d evolved into abstract form. Only number 1 still closely resembles a tally.

Another thing needed for a positional system to work is the invention of zero.

It’s hard to appreciate how much our positional number system depends on the zero. In 30, we know that the 3 means “three tens” because it’s in the tens place. But how do we know it’s in the tens place? How can we show it in the tens place if there was nothing in the ones place?

In early positional system, people would just leave the ones place blank. The Babylonians tried this, and it led to predictable problems:

Since scribes could easily overlook it in copying, through fatigue or carelessness. Moreover, it was difficult to indicate precisely the absence of two or more consecutive orders of magnitude, since one empty space beside another empty space is not easily distinguished from a single empty space.

Zero might not seem a hard concept to those of us who have grown up with it. But the idea of making a number to mean “nothing” — a number for that without number — is so nonintuitive that it only happened three times independently: Among the Maya, the Babylonians, and the Indians. And of these three, it was the Indians that wound up giving us our modern numbers.

Thank You, India

Was there anything special about India that explains why the modern system evolved there? Ifrah proposes that ancient Indians had an affinity for really big numbers:

The early passion which Indian civilization had for high numbers was a significant factor contributing to the discovery of the place-value system and not only offered the Indians the incentive to go beyond the ‘calculable’ physical world, but also led to an understanding (much earlier than in our civilization) of the notion of mathematical infinity itself.

He quotes as examples early Buddhist texts that mention “ten thousand monks, eighty-four million Apsaras, thirty-two thousand Bodhisattvas, sixty-eight thousand Brahmas, a million Shakras, a hundred-thousand gods, hundreds of millions of divinities….” He also notes that, in the Bhagavad Gita, the length of Brahma’s life is given as 311,040,000,000,000 human years, with commentaries pointing out that this seems like infinity to us, but relative to eternity it is nothing.

Whether cause or effect of this fascination with huge numbers, the Sanskrit language developed a number system that gave a distinct name to every power of ten. This is very unusual: Other cultures ran out of unique number words around a thousand or so. In ancient Arabic, for instance, you said 198 billion as (roughly translated) “a hundred thousand thousand thousand and nine-eight thousand thousand thousand.”

Our modern way — one hundred and ninety-eight billion — is more elegant, but in a way, it also is topping out after a thousand: thousand, like million and billion, functions as an auxiliary base. It allows us to go back to recycling the names we used for lower numbers, so don’t need to learn any new number names between a thousand and a million. Counting after a thousand is the same as counting to a thousand, except you say “thousand” at the end.

In Sanskrit, you did have to keep learning new names. That might have made learning to count more difficult, but it also paved the way for discovering the positional system.

The role of language is a surprising theme in this book. As much as we nowadays think of numbers and words as quite distinct, something that stands out about Ifrah’s account is how much the evolution of language drove the evolution of number. Numbers have their origin in spoken counting systems, and in the practical problems of naming quantities and, in the case of Sanskrit, of writing names.

For in ancient India, the great astronomers and mathematicians didn’t yet write their findings with the Brahmi numerals: They wrote them with the Sanskrit words.¹ Thus the number 251,567,183 would be written something like (translating and parsing), “two hundred-millions and five ten-millions and one million and five hundred-thousands and six ten-thousands and seven thousands and one hundreds and eight tens and three ones.”

For a people who liked huge numbers and who were developing complex math, this way of writing numbers took up a lot of space and meant a lot of wasted time finding and drying palm leaves to write upon. There was incentive to find a shorter way.

So Indian scholars began abbreviating the number expression by leaving out the terms for each factor of ten: Instead of saying “five hundreds, six tens, and three ones” they’d just say “five, six, three.” It was understood by position that “five” meant “five hundreds.” By shortening their sentences, they invented the positional system.

With the evolution of the positional system, the need for a zero became apparent, and here too Indian culture seemed pre-adapted to the task: Sanskrit had a rich vocabulary of words for “void” or “absence,” and there was a body of mystical and religious philosophy dealing with the concept as an element of being. A people used to contemplating nothing didn’t have much difficulty applying one of those Sanskrit words for it to their written expression of numbers. At first zero was just as a placeholder, but eventually mathematicians decided that it was a weird sort of number in its own right — the number of nothing.

But at this stage, the numbers were still just words. How did those Brahmi numerals come back into the picture?

Since you can’t do written math with words, ancient Indians relied on the abacus just as much as every other ancient civilization did. The key difference is that the Indian abacus itself involved writing.

The Indian scholars used a dust abacus. Instead of physical tokens like stones or beads, they drew their counting tokens on a table covered in fine dust. The table was divided into columns, each column representing a power of ten. And how did they indicate which quantity went into each column? Instead of using beads of different color or size, they just drew the Brahmi numerals: 1, 2, 3, 4….

And now we’re very close to the modern system, because the Indian mathematician using his dust abacus would enter the number 8,675 as: / 8 / 6 / 7 / 5 /.

The last big step was for some scholar, seeking to further economize his written expression, to realize that instead of writing the abbreviated Sanskrit number words on his palm leaf, he could just write the Brahmi numerals.

And once he did that, he effectively had his abacus on the palm leaf. The columns were gone, but with the rule of position and the zero, they weren’t needed. Now the mathematical algorithms that used to require the dust abacus only required a writing surface and writing tool. It’s not so much that the abacus became obsolete; it’s that it escaped containment.

The Triumph of Numbers

The modern number system had more or less solidified in India by the fifth century A.D.

From India it spread outward. Mongols would eventually adopt Indian numbers by way of the Tibetans, despite getting their writing system from elsewhere. The Muslim conquests and flowering of Islamic civilization brought the numbers Westward. Muslim scholars further developed the Indian math: Mathematician Muhammad al-Khwarizmi generalized the rules of written arithmetic, becoming the father of algebra. The Europeans who adopted the numbers from the Muslim world named the technique for written arithmetic after al-Khwarizmi, calling it “algorism” — the root of our word algorithm.

Both the numbers and algorism gained a foothold in Europe after the Crusades, but met stiff resistance from the abacists — a powerful professional group who did not want to see their hard-won abacus skills devalued. All the same, by the 1200s, the algorists were gaining ground, and written arithmetic slowly but surely spread.

And it continued to spread. Written math probably peaked in the middle of the twentieth century, before handheld electronic calculators became widespread enough to partially supplant paper. But the calculators still bear the same numbers, and the numbers are likely to last.

If you’d like to support Bullfish Hole, you can leave a tip at this Stripe link. Or become a subscriber with the button below.

1. The line between the verbal and the mathematical was especially blurred in ancient India, where astronomers and mathematicians were also poets. They recorded their numerical findings not just with words, but with verse, and used colorful symbolic words (“arms of Vishnu”) in place of the ordinary number terms. The verses were preferred for mnemonic reasons, and because, at this time, the Brahmi numerals, while widespread, weren’t standardized across regions. Verses were less ambiguous, and also less prone to copying errors — mess up a number and you might not notice, mess up a verse and suddenly the rhythm doesn’t work.